考虑哪些因素会导致酒店预订被取消
取消预订的原因可能有多种。例如,客户可能要求提供不可用的服务(如停车位),客户可能后来发现酒店不符合他们的要求,或者客户可能只是取消了整个行程。其中一些情况(如停车场)可由酒店采取行动,而其他情况(如行程取消)则不在酒店的控制范围内。无论如何,我们希望更好地了解哪些因素导致了预订取消。
模拟案例 读取数据 1 2 3 import pandas as pddataset = pd.read_csv('Z:/TData/big-data/SADAGY/251021_causal_inference_booking_cancellation.csv' )
1 2 3 4 5 6 7 8 9 10 dataset.head() Out[8]: hotel is_canceled ... reservation_status reservation_status_date 0 Resort Hotel 0 ... Check-Out 2015-07-01 1 Resort Hotel 0 ... Check-Out 2015-07-01 2 Resort Hotel 0 ... Check-Out 2015-07-02 3 Resort Hotel 0 ... Check-Out 2015-07-02 4 Resort Hotel 0 ... Check-Out 2015-07-03 [5 rows x 32 columns]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 dataset.columns Out[7]: Index(['hotel', 'is_canceled', 'lead_time', 'arrival_date_year', 'arrival_date_month', 'arrival_date_week_number', 'arrival_date_day_of_month', 'stays_in_weekend_nights', 'stays_in_week_nights', 'adults', 'children', 'babies', 'meal', 'country', 'market_segment', 'distribution_channel', 'is_repeated_guest', 'previous_cancellations', 'previous_bookings_not_canceled', 'reserved_room_type', 'assigned_room_type', 'booking_changes', 'deposit_type', 'agent', 'company', 'days_in_waiting_list', 'customer_type', 'adr', 'required_car_parking_spaces', 'total_of_special_requests', 'reservation_status', 'reservation_status_date'], dtype='object')
特征工程 接下来可以创建一些新的有意义的特征,以减少数据集的维度。例如,总住宿天数 = stays_in_weekend_nights + stays_in_week_nights;客人数量 = adults + children + babies;是否分配了不同的房间 = 如果 reserved_room_type 与 assigned_room_type 不同,则为 1,否则为 0。
1 2 3 4 5 6 7 8 9 10 11 12 13 dataset['total_stay' ] = dataset['stays_in_week_nights' ] + dataset['stays_in_weekend_nights' ] dataset['guests' ] = dataset['adults' ] + dataset['children' ] + dataset['babies' ] dataset['different_room_assigned' ] = 0 slice_indices = dataset['reserved_room_type' ] != dataset['assigned_room_type' ] dataset.loc[slice_indices, 'different_room_assigned' ] = 1 dataset = dataset.drop(['stays_in_week_nights' , 'stays_in_weekend_nights' , 'adults' , 'children' , 'babies' , 'reserved_room_type' , 'assigned_room_type' ], axis = 1 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 dataset.columns Out[9]: Index(['hotel', 'is_canceled', 'lead_time', 'arrival_date_year', 'arrival_date_month', 'arrival_date_week_number', 'arrival_date_day_of_month', 'stays_in_weekend_nights', 'stays_in_week_nights', 'adults', 'children', 'babies', 'meal', 'country', 'market_segment', 'distribution_channel', 'is_repeated_guest', 'previous_cancellations', 'previous_bookings_not_canceled', 'reserved_room_type', 'assigned_room_type', 'booking_changes', 'deposit_type', 'agent', 'company', 'days_in_waiting_list', 'customer_type', 'adr', 'required_car_parking_spaces', 'total_of_special_requests', 'reservation_status', 'reservation_status_date'], dtype='object')
删除了包含 NULL 值或具有过多唯一值的其他列(例如,代理 ID)。还用出现频率最高的国家来填补缺失的值。
由于与 country、distribution_channel 和 market_segment 有很高的重叠,将其删除:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 # 检查数据集中的缺失值 dataset.isnull().sum() Out[10]: hotel 0 is_canceled 0 lead_time 0 arrival_date_year 0 arrival_date_month 0 arrival_date_week_number 0 arrival_date_day_of_month 0 stays_in_weekend_nights 0 stays_in_week_nights 0 adults 0 children 4 babies 0 meal 0 country 488 market_segment 0 distribution_channel 0 is_repeated_guest 0 previous_cancellations 0 previous_bookings_not_canceled 0 reserved_room_type 0 assigned_room_type 0 booking_changes 0 deposit_type 0 agent 16340 company 112593 days_in_waiting_list 0 customer_type 0 adr 0 required_car_parking_spaces 0 total_of_special_requests 0 reservation_status 0 reservation_status_date 0 dtype: int64
‘country’, ‘agent’, ‘company’ 这三列分别包含 488, 16340, 112593 个缺失值。这里删除 ‘agent’ 和 ‘company’ 列;用出现频率最高的国家填充缺失的 ‘country’ 列。
1 2 3 4 5 dataset = dataset.drop(['agent' , 'company' ], axis = 1 ) dataset['country' ] = dataset['country' ].fillna(dataset['country' ].mode()[0 ])
1 2 3 4 5 6 7 8 dataset = dataset.drop(['reservation_status' , 'reservation_status_date' , 'arrival_date_day_of_month' ], axis = 1 ) dataset = dataset.drop(['arrival_date_year' ], axis = 1 ) dataset = dataset.drop(['distribution_channel' ], axis = 1 )
1 2 3 4 5 6 7 8 9 10 11 12 13 dataset = dataset.drop(['distribution_channel' ], axis = 1 ) dataset['different_room_assigned' ] = dataset['different_room_assigned' ].replace(1 , True ) dataset['different_room_assigned' ] = dataset['different_room_assigned' ].replace(0 , False ) dataset['is_canceled' ] = dataset['is_canceled' ].replace(1 , True ) dataset['is_canceled' ] = dataset['is_canceled' ].replace(0 , False ) dataset.dropna(inplace = True )
1 2 3 4 5 6 7 8 9 10 dataset.columns Out[15]: Index(['hotel', 'is_canceled', 'lead_time', 'arrival_date_month', 'arrival_date_week_number', 'meal', 'country', 'market_segment', 'is_repeated_guest', 'previous_cancellations', 'previous_bookings_not_canceled', 'booking_changes', 'deposit_type', 'days_in_waiting_list', 'customer_type', 'adr', 'required_car_parking_spaces', 'total_of_special_requests', 'total_stay', 'guests', 'different_room_assigned'], dtype='object')
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 dataset.iloc[:, 5:20].head(100) Out[16]: meal country market_segment ... total_of_special_requests total_stay guests 0 BB PRT Direct ... 0 0 2.0 1 BB PRT Direct ... 0 0 2.0 2 BB GBR Direct ... 0 1 1.0 3 BB GBR Corporate ... 0 1 1.0 4 BB GBR Online TA ... 1 2 2.0 .. ... ... ... ... ... ... ... 95 BB PRT Online TA ... 1 2 2.0 96 BB PRT Online TA ... 1 7 2.0 97 HB ESP Offline TA/TO ... 1 7 3.0 98 BB PRT Online TA ... 2 7 3.0 99 BB DEU Direct ... 0 7 2.0 [100 rows x 15 columns]
1 2 dataset = dataset[dataset.deposit_type == "No Deposit" ]
1 2 3 4 5 6 7 8 9 10 In [17]: # 按照 'deposit_type' 和 'is_canceled' 列分组,并计算每个组合的计数 dataset.groupby(['deposit_type', 'is_canceled']).count() Out[17]: hotel lead_time ... guests different_room_assigned deposit_type is_canceled ... No Deposit False 74947 74947 ... 74947 74947 True 29690 29690 ... 29690 29690 [2 rows x 19 columns]
1 dataset_copy = dataset.copy(deep = True )
计算预期计数 由于取消次数和分配不同房间的次数严重失衡,我们首先随机选择 1000 个观察值,查看在多少情况下变量 is_cancelled 和 different_room_assigned 具有相同的值。然后,这个过程重复 10000 次,预期结果接近 50%(即这两个变量随机取得相同值的概率)。
从统计学角度来看,在这个阶段我们无法得出明确的结论。因此,分配与客户之前预定时不同的房间,可能会导致他/她取消预订,也可能不会。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 counts_sum = 0 for i in range (1 , 10000 ): counts_i = 0 rdf = dataset.sample(1000 ) counts_i = rdf[rdf["is_canceled" ] == rdf["different_room_assigned" ]].shape[0 ] counts_sum += counts_i counts_sum / 10000
现在,我们考虑没有预订更改的场景,并重新计算预期计数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 counts_sum = 0 for i in range (1 , 10000 ): counts_i = 0 rdf = dataset[dataset["booking_changes" ] == 0 ].sample(1000 ) counts_i = rdf[rdf["is_canceled" ] == rdf["different_room_assigned" ]].shape[0 ] counts_sum += counts_i counts_sum / 10000
在第二种情况下,我们采用存在预订更改 ( >0 ) 的场景,并重新计算预期计数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 counts_sum = 0 for i in range (1 , 10000 ): counts_i = 0 rdf = dataset[dataset["booking_changes" ] > 0 ].sample(1000 ) counts_i = rdf[rdf["is_canceled" ] == rdf["different_room_assigned" ]].shape[0 ] counts_sum += counts_i counts_sum / 10000 
当预订更改的数量不为零时,肯定会发生一些变化。因此,它暗示了 Booking Changes 可能会影响客房取消。
但是 Booking Changes 是唯一令人困惑的变量吗?如果有一些未观察到的混杂因素,我们的数据集中没有关于这些信息(特征)怎么办。我们还能像以前一样提出索赔吗?
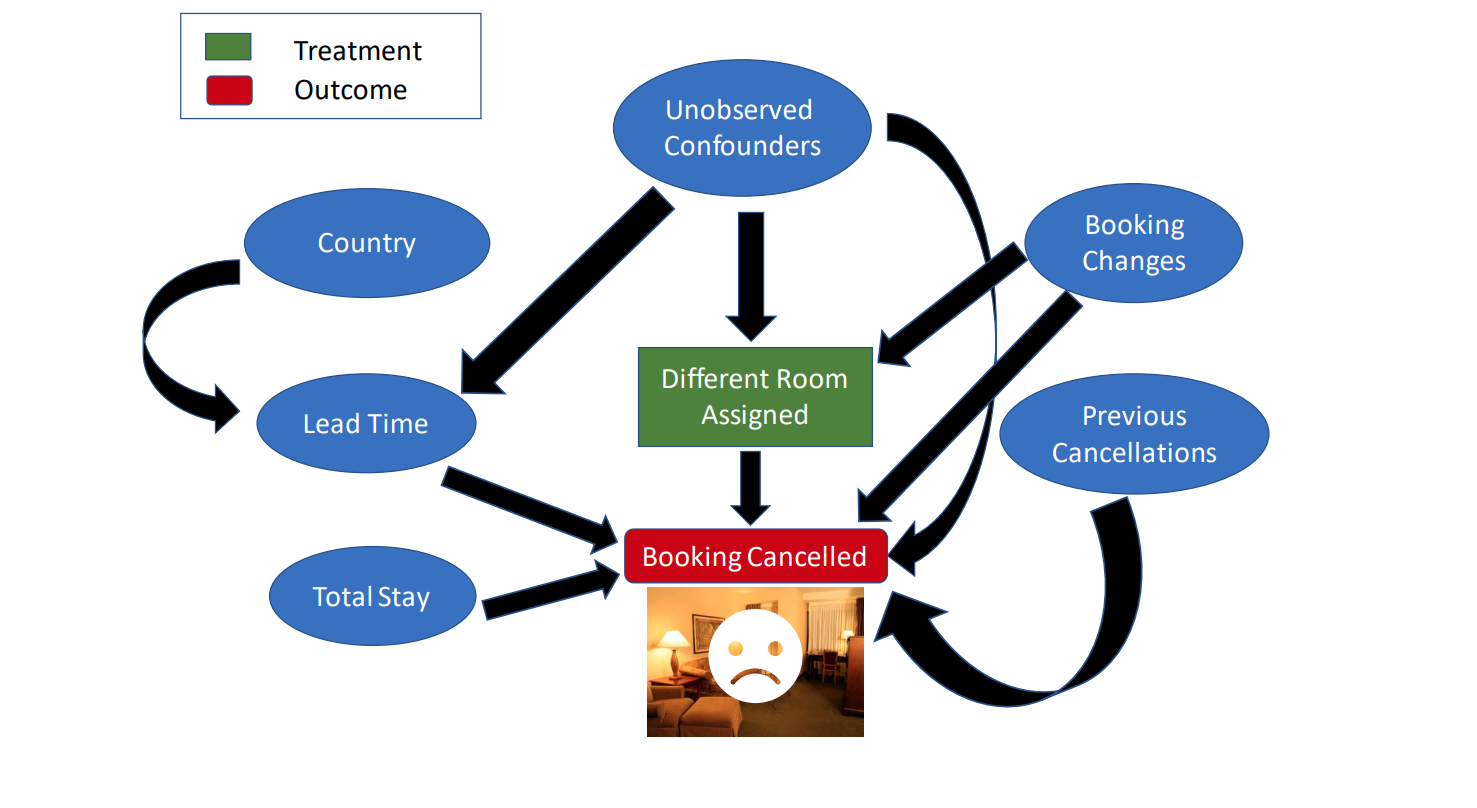
使用 DoWhy 估计因果效应 创建因果图 以下是关于预测建模问题的假设,并将其转换为因果图(Causal Diagram)的列表:
市场细分有两个级别,TA 指的是旅行代理商 ,而 TO 指的是旅游运营商 ,因此它会影响提前时间(Lead Time),即预订和到达之间的天数。
国家也会在决定一个人是否提前预定(因此更长的提前时间)以及他/她偏好哪种餐饮类型上发挥作用。
提前时间无疑会影响等待名单天数(Days in Waitlist),如果你晚些预定,找到空房的机会较小。此外,更长的提前时间也可能导致取消预订。
等待名单天数、总住宿天数和客人数量可能会影响预订是否被取消或保留。
过去的预订保留记录会影响一个客户是否会保留预订。此外,这两个变量都会影响预订是否会被取消(例如:一个过去保留了五次预订的客户,这次也更有可能保留;同样,曾经取消过预订的客户,这次也更可能再次取消)。
预订变更会影响客户是否被分配到不同的房间,这也可能导致取消预订。
最后,预订变更作为唯一影响处理和结果的变量是不太可能的,可能存在一些未观察到的混杂因素,关于这些因素,我们的数据中没有任何信息。
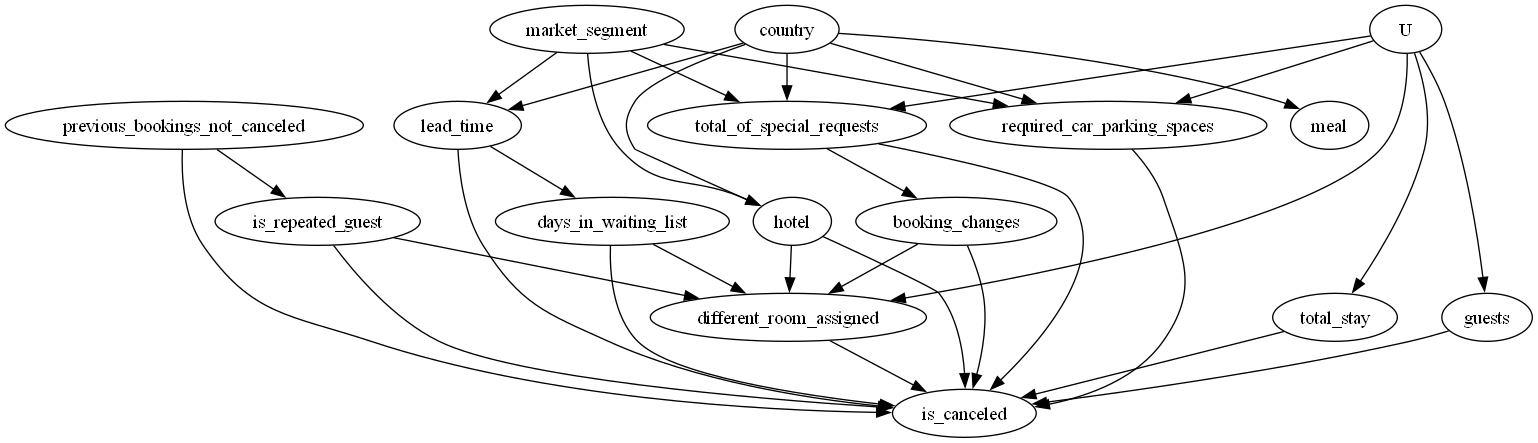
定义图中的节点及其标签 1 2 3 4 5 6 7 8 9 10 11 12 13 14 different_room_assigned[label='Different Room Assigned' ]; is_canceled[label='Booking Cancelled' ]; booking_changes[label='Booking Changes' ]; previous_bookings_not_canceled[label='Previous Booking Retentions' ]; days_in_waiting_list[label='Days in Waitlist' ]; lead_time[label='Lead Time' ]; market_segment[label='Market Segment' ]; country[label='Country' ]; U[label='Unobserved Confounders' ,observed='no' ]; is_repeated_guest; total_stay; guests; meal; hotel;
定义隐性关系,表示哪些变量之间有因果关系 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 U->{different_room_assigned,required_car_parking_spaces,guests,total_stay,total_of_special_requests}; market_segment -> lead_time; lead_time -> is_canceled; country -> lead_time; different_room_assigned -> is_canceled; country -> meal; lead_time -> days_in_waiting_list; days_in_waiting_list -> {is_canceled, different_room_assigned}; previous_bookings_not_canceled -> is_canceled; previous_bookings_not_canceled -> is_repeated_guest; is_repeated_guest -> {different_room_assigned, is_canceled}; total_stay -> is_canceled; guests -> is_canceled; booking_changes -> different_room_assigned; booking_changes -> is_canceled; hotel -> {different_room_assigned, is_canceled}; required_car_parking_spaces -> is_canceled; total_of_special_requests -> {booking_changes, is_canceled}; country -> {hotel, required_car_parking_spaces, total_of_special_requests}; market_segment -> {hotel, required_car_parking_spaces, total_of_special_requests}; }
代码实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 import dowhyfrom IPython.display import Image, displaycausal_graph = '''digraph { different_room_assigned[label="Different Room Assigned"]; is_canceled[label="Booking Cancelled"]; booking_changes[label="Booking Changes"]; previous_bookings_not_canceled[label="Previous Booking Retentions"]; days_in_waiting_list[label="Days in Waitlist"]; lead_time[label="Lead Time"]; market_segment[label="Market Segment"]; country[label="Country"]; U[label="Unobserved Confounders",observed="no"]; is_repeated_guest; total_stay; guests; meal; hotel; U->{different_room_assigned,required_car_parking_spaces,guests,total_stay,total_of_special_requests}; market_segment -> lead_time; lead_time->is_canceled; country -> lead_time; different_room_assigned -> is_canceled; country->meal; lead_time -> days_in_waiting_list; days_in_waiting_list ->{is_canceled,different_room_assigned}; previous_bookings_not_canceled -> is_canceled; previous_bookings_not_canceled -> is_repeated_guest; is_repeated_guest -> {different_room_assigned,is_canceled}; total_stay -> is_canceled; guests -> is_canceled; booking_changes -> different_room_assigned; booking_changes -> is_canceled; hotel -> {different_room_assigned,is_canceled}; required_car_parking_spaces -> is_canceled; total_of_special_requests -> {booking_changes,is_canceled}; country->{hotel, required_car_parking_spaces,total_of_special_requests}; market_segment->{hotel, required_car_parking_spaces,total_of_special_requests}; }''' model = dowhy.CausalModel( data = dataset, graph = causal_graph.replace("\n" , " " ), treatment = "different_room_assigned" , outcome = 'is_canceled' ) model.view_model(file_name = 'C:/Users/Administrator/Desktop/causal_model' ) display(Image(filename = "C:/Users/Administrator/Desktop/causal_model.png" ))
确定因果效应 处理 (Treatment) 导致结果 (Outcome),如果改变处理会导致结果发生变化,同时保持其他因素不变。因此,在这一步中,通过利用因果图的属性,我们识别出需要估计的因果效应。
1 2 3 4 5 identified_estimand = model.identify_effect(proceed_when_unidentifiable = True ) print (identified_estimand)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Estimand type: nonparametric-ate ### Estimand : 1 Estimand name: backdoor Estimand expression: d ↪ ──────────────────────────(E[is_canceled|hotel,is_repeated_guest,lead_time,total_stay,guests,required_car_parking_spaces,booking_changes,days_in_waiting_list,total_of_special_requests]) ↪ d[different_room_assigned] ↪ Estimand assumption 1, Unconfoundedness: If U→{different_room_assigned} and U→is_canceled then P(is_canceled|different_room_assigned,hotel,is_repeated_guest,lead_time,total_stay,guests,required_car_parking_spaces,booking_changes,days_in_waiting_list,total_of_special_requests,U) = P(is_canceled|different_room_assigned,hotel,is_repeated_guest,lead_time,total_stay,guests,required_car_parking_spaces,booking_changes,days_in_waiting_list,total_of_special_requests) ### Estimand : 2 Estimand name: iv No such variable(s) found! ### Estimand : 3 Estimand name: frontdoor No such variable(s) found!
输出分为三个部分,dowhy尝试了三种主要的因果效应识别测量:后门 (backdoor) 、工具变量 (IV) 和 前门 (frontdoor) 。
Estimand type: nonparametric-ate
nonparametric (非参数),这意味着dowhy在识别因果效应时,没有对变量之间的函数关系做任何特定假设, 例如,不假设它们是线性关系。这使得模型更加灵活和普适。
ate (Average Treatment Effect,平均处理效应),这是想要的估计目标。ATE 回答的是这样一个问题:“如果我们对总体中的每一个人都进行处理(即都分配不同的房间),然后我们再对总体中的每一个人都不进行处理(即都分配预订的房间),这两种情况下,平均取消率的差异是多少?” 这是一个衡量处理变量对整个总体平均影响的指标。
### Estimand : 1
↪
这是最重要的结果,因为它成功地找到了一个识别方法。Estimand name: backdoordowhy 成功地应用了后门准则。在这个因果图中,从处理变量 different_room_assigned 到结果变量 is_canceled,除了我们关心的直接路径 different_room_assigned -> is_canceled 之外,还存在一些后门路径。这些路径通常包含一个指向 different_room_assigned 的箭头,并且通过一个或多个中间变量最终指向 is_canceled。例如,different_room_assigned <- booking_changes -> is_canceled 就是一条典型的后门路径。
为什么后门路径是问题? 这些路径引入了混淆偏倚 (Confounding Bias)。booking_changes (预订变更次数) 既可能影响酒店是否给你换房间,也可能直接影响你是否最终会取消。如果直接比较“换了房间”和“没换房间”两组人的取消率,我们无法分清这个差异到底是多少由“换房间”本身引起的,又有多少是由“预订变更”这个共同原因引起的。
后门准则告诉我们,如果我们能找到一组变量 (称为“后门变量集”),并对它们进行统计控制 (conditioning on),从而“关闭”所有这些后门路径,那么我们就可以消除混淆偏倚,分离出纯粹的因果效应。
Estimand expression 1 2 3 4 Estimand expression: # 估算表达式 d ↪ ──────────────────────────(E[is_canceled|hotel,...,booking_changes,days_in_waiting_list,total_of_special_requests]) ↪ d[different_room_assigned]
这是dowhy给出的“配方”。
E[is_canceled| ... ] 表示在给定一系列变量的条件下,is_canceled 的期望值(或平均值)。
d/d[different_room_assigned] 是微积分中的导数符号,在这里它代表了当我们干预 different_room_assigned 时,is_canceled 期望值的变化率。对于二元处理变量(0/1),可以将其理解为 E[is_canceled | do(treatment=True)] - E[is_canceled | do(treatment=False)],也就是 ATE。
最重要的部分 :括号 | 后面的变量列表:hotel, is_repeated_guest, ... , total_of_special_requestsdowhy 根据因果图找到的需要被控制的混淆变量集 。这个表达式的含义是:要计算 different_room_assigned 对 is_canceled 的因果效应,你需要通过统计方法(如分层、匹配、回归)来控制(或调整)以上所有这些变量的影响。
Estimand assumption 1 1 Estimand assumption 1, Unconfoundedness: If U→{different_room_assigned} and U→is_canceled then P(is_canceled|different_room_assigned,hotel,is_repeated_guest,lead_time,total_stay,guests,required_car_parking_spaces,booking_changes,days_in_waiting_list,total_of_special_requests,U) = P(is_canceled|different_room_assigned,hotel,is_repeated_guest,lead_time,total_stay,guests,required_car_parking_spaces,booking_changes,days_in_waiting_list,total_of_special_requests)
Unconfoundedness (无混淆假设): 这是使用后门准则必须满足的核心假设。
If U→{different_room_assigned} and U→is_canceled ... 这里的 U 代表您在图中定义的“未观测到的混淆因素 (Unobserved Confounders)”。这个假设的含义是:“承认可能存在一些我们没有观测到的、同时影响‘换房间’和‘取消预订’的因素 U。但是,我们假设 ,只要我们控制了表达式中列出的那一长串可观测 的变量,那么 U 的影响就可以被忽略不计了。”
换句话说,它假设没有未被观测到的混淆因素 。这是一个非常强的假设,并且无法通过数据来检验 。它的合理性完全取决于作为领域专家的知识和所画的因果图的准确性。如果存在一个重要的、未被观测的共同原因(例如,某个特定日期的酒店超售政策,这个信息不在数据里),那么这个假设就不成立,估计结果就会有偏。
Instrumental Variable 1 2 3 ### Estimand : 2 Estimand name: iv # 工具变量 No such variable(s) found!
Estimand name: iv: dowhy 尝试寻找一个或多个工具变量。
No such variable(s) found!不存在任何一个变量满足工具变量的严格定义 。例如,booking_changes 虽然影响 different_room_assigned,但它也直接影响 is_canceled,所以它不能作为工具变量。因此,IV 方法在这里不适用。
Frontdoor 1 2 3 ### Estimand : 3 Estimand name: frontdoor No such variable(s) found!
Estimand name: frontdoor: dowhy 尝试应用前门准则。
No such variable(s) found!: 这个结果意味着,在因果图中,不存在满足前门准则所要求的中介变量结构 。因此,前门方法在这里也不适用。
核心结论 根据提供的因果图,dowhy 告诉:
因果效应是可识别的 (Identifiable) :这是一个好消息!这意味着从理论上讲,可以使用您的数据来估计“换房间”对“取消预订”的因果效应。唯一的识别策略是后门调整 (Backdoor Adjustment) :必须通过控制一组特定的混淆变量来计算这个效应。工具变量和前门方法不适用 :因果图结构不支持这两种方法。
但需要注意的是:所有这些结论的有效性都建立在因果图是正确的前提下。 如果因果图有误(例如,遗漏了重要的混淆变量,或者画错了箭头的方向),那么即使 dowhy 给出结果,这个结果也可能是错误的。因果推断的挑战不仅在于计算,更在于建立一个符合现实的因果模型。
估计已识别的估计值和 1 2 3 4 5 6 7 8 9 10 11 12 estimate = model.estimate_effect( identified_estimand, method_name = "backdoor.propensity_score_weighting" , target_units = "ate" ) print (estimate)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 *** Causal Estimate *** ## Identified estimand Estimand type: nonparametric-ate ### Estimand : 1 Estimand name: backdoor Estimand expression: d ↪ ──────────────────────────(E[is_canceled|hotel,is_repeated_guest,lead_time,total_stay,guests,required_car_parking_spaces,booking_changes,days_in_waiting_list,total_of_special_requests]) ↪ d[different_room_assigned] ↪ Estimand assumption 1, Unconfoundedness: If U→{different_room_assigned} and U→is_canceled then P(is_canceled|different_room_assigned,hotel,is_repeated_guest,lead_time,total_stay,guests,required_car_parking_spaces,booking_changes,days_in_waiting_list,total_of_special_requests,U) = P(is_canceled|different_room_assigned,hotel,is_repeated_guest,lead_time,total_stay,guests,required_car_parking_spaces,booking_changes,days_in_waiting_list,total_of_special_requests) ## Realized estimand b: is_canceled~different_room_assigned+hotel+is_repeated_guest+lead_time+total_stay+guests+required_car_parking_spaces+booking_changes+days_in_waiting_list+total_of_special_requests Target units: ate ## Estimate Mean value: -0.2621202162797218
Identified estimand 这部分内容与上一步 model.identify_effect() 的输出是完全一样的。dowhy 在这里再次展示它,是为了提醒,接下来的所有数值计算都建立在这个理论基础之上。
Realized estimand 1 2 3 ## Realized estimand # 已实现的估算量/实践方法 b: is_canceled~different_room_assigned+hotel+is_repeated_guest+lead_time+... Target units: ate
描述了 dowhy 是如何根据选择的 method_name="backdoor.propensity_score_weighting"(倾向性得分加权法),将理论上的“后门”准则转化为一个具体的统计模型的。
b: is_canceled ~ ...dowhy 实际执行了以下步骤:
建立倾向性得分模型 :首先,dowhy 建立了一个模型来预测处理变量本身 。它实际拟合的模型是 different_room_assigned ~ hotel + is_repeated_guest + ...。这个模型的目的是计算每个订单被“分配不同房间”的概率,这个概率就是倾向性得分 (Propensity Score) 。计算权重 :然后,dowhy 使用这些倾向性得分给数据集里的每一行(每个订单)分配一个权重。这些权重的目标是创建一个新的、统计意义上的“伪人群”,在这个“伪人群”中,被分配了不同房间的“处理组”和没有被分配不同房间的“对照组”,在所有指定的混淆变量上都是完美平衡的。对于ATE(平均处理效应),处理组的权重通常是 1 / 倾向性得分,对照组的权重是 1 / (1 - 倾向性得分)。计算加权平均值 :最后,dowhy 在这个经过加权调整的“伪人群”中,计算处理组和对照组之间结果变量 (is_canceled) 的平均值差异。
Target units: ate平均处理效应 (Average Treatment Effect) ,即该因果效应对您数据集中定义的整个群体(此处为“无押金”的预订)的平均影响。
Estimate 1 2 ## Estimate Mean value: -0.2621202162797218
这是您整个因果分析的最终量化结果,也就是估算出的平均处理效应(ATE)。由于结果变量 is_canceled 是一个二元变量(True=1, False=0),这个数字代表了概率的变化:在控制了所有指定的混淆因素之后,为顾客分配一个与预订时不同的房间,这一行为会导致取消预订的概率平均下降 26.21 个百分点 。
让我们把这个结论具体化:
想象有两组完全相同的顾客(他们在 hotel, lead_time, guests, booking_changes 等所有混淆变量上都一模一样)。
A 组顾客得到了他们预订的房间。
B 组顾客被分配了不同的房间。
这个结果预测,B 组的取消率将会比 A 组 低 26.21 个百分点 。
核心结论 估算的平均处理效应值为 -0.262。这个结果意味着,如果分配不同房间 (different_room_assigned),则取消预订的概率会减少约 26.2%。负值表示分配不同房间可能降低取消预订的几率。
从因果效应的估算来看,分配不同的房间different_room_assigned似乎会减少取消预订的概率is_canceled。这个结果与之前的关联分析中发现的正相关不同,表明可能存在其他机制或未观察到的变量在起作用。例如,分配不同房间可能只发生在房间不可用时,或者发生在入住时,可能会影响顾客的体验,降低取消的概率。
结果令人惊讶,这意味着分配不同的房间会减少取消预订的概率 。这里有更多的内容需要解读:**这是正确的因果效应吗?**是否可能是因为只有在预定的房间不可用时才会分配不同的房间,因此分配不同的房间实际上对顾客有积极影响(与不分配房间相比)?也许还有其他机制在起作用 。或许,只有在入住时才会分配不同的房间,而一旦顾客已经到达酒店,取消预订的概率就会很低?在这种情况下,图中缺少了一个关键变量,即这些事件发生的时间。是否大部分发生在预订当天?知道这个变量可以帮助改善图形和我们的分析。
虽然之前的关联分析显示了不同房间分配与取消预订之间的正相关,但使用 DoWhy 估算因果效应则呈现出不同的图景 。它暗示,减少酒店中不同房间分配的决策或政策可能适得其反。
反驳结果 请注意,因果部分并非来自数据,而是来自于用于识别的假设,数据仅用于统计估算。
因此,验证我们在第一步中所做的假设是否正确变得至关重要!
如果存在另一个共同原因,会发生什么?如果处理本身是安慰剂,会发生什么?
方法一,随机共同原因 随机共同原因:向数据中添加随机抽取的协变量,并重新运行分析,看看因果估计是否发生变化。如果最初的假设是正确的,那么因果估计应该不会发生太大变化。
1 2 3 4 5 6 7 8 9 refute1_results = model.refute_estimate( identified_estimand, estimate, method_name = "random_common_cause" ) print (refute1_results)
1 2 3 4 Refute: Add a random common cause Estimated effect:-0.2621202162797218 New effect:-0.26221394657576885 p value:0.26
这个反驳结果表明,通过引入一个随机共同原因来测试因果估算的稳健性,得到了以下结果:
Estimated effect (-0.2621202162797218): 这是原始的因果估算结果。它量化了“分配不同房间” (different_room_assigned) 对“是否取消预订” (is_canceled) 的因果效应。该数值表明,分配不同房间这一行为,平均会导致 取消预订的概率下降约 26.21 个百分点 。
New effect (-0.26221394657576885): 这是在模型中加入一个完全随机的变量(并将其伪装成一个混淆变量)后,重新计算出的因果效应值。通过对比可以发现,新的效应值与原始效应值几乎完全相同,差异小到可以忽略不计。
p value (0.26): p 值为 0.26。在统计学上,p 值检验的是“新旧效应值之间没有差异”这一零假设。它表明 新旧效应值之间的微小差异完全是随机的,二者在统计上没有任何显著区别。这证实了引入的随机变量对因果估算结果没有产生任何实际影响 。
核心结论:由于在模型中添加一个随机共同原因后,估算出的因果效应值几乎没有发生任何变化,并且 p 值为 0.26(大于常规的显著性水平 0.05),这说明我们的因果估算结果成功通过了此次反驳检验 。
这个检验就像一个“安慰剂测试”:给模型加入一个已知的、无效的“干扰项”,看模型是否会产生错误的反应。结果表明,模型没有产生任何反应。这有力地证明了我们的因果估算模型是稳健的 (robust) ,不会因为数据中无关的随机噪声而轻易动摇。因此,我们可以更加确信,原始估算出的 -0.2621 这个效应值是可靠且稳定的。
方法二,安慰剂处理反驳器 安慰剂处理反驳器:随机将任意协变量作为处理分配,并重新运行分析。如果我们的假设是正确的,那么新计算出的估算值应该接近 0 。
1 2 3 4 5 6 7 8 9 refute2_results = model.refute_estimate( identified_estimand, estimate, method_name = "placebo_treatment_refuter" ) print (refute2_results)
1 2 3 4 Refute: Use a Placebo Treatment Estimated effect:-0.2621202162797218 New effect:0.00017360667244984917 p value:0.96
这个反驳结果使用了 安慰剂处理反驳器 (Placebo Treatment Refuter) 的方法来测试因果模型的可靠性。
该方法的核心思想是:如果我们的模型真的能够识别因果关系,那么它应该能够正确地识别出“没有因果关系”的情况。
检验过程是:dowhy 暂时忽略掉真实的“处理变量” (different_room_assigned),而是从数据中随机挑选另一个变量(或生成一个随机变量)作为“安慰剂处理”(即假的处理变量),然后重新运行整个因果效应估算流程,计算这个“安慰剂”对结果变量 is_canceled 的“因果效应”。
Estimated effect (-0.2621202162797218): 这是原始的、核心的因果估算结果。它表明,分配不同房间这一真实的处理行为,会导致取消预订的概率平均下降 26.21 个百分点。
New effect (0.00017360667244984917): 这是使用“安慰剂处理”后计算出的新“因果效应”。这个数值非常非常小,极其接近于 0。它大约等于 +0.00017,意味着这个安慰剂处理“导致”取消率上升了 0.017 个百分点,这是一个在实际业务中完全可以忽略不计的、几乎为零的影响。
p value (0.96): 这个 p 值在这里至关重要。它检验的“零假设”是:“这个新计算出的安慰剂效应值等于 0” 。
您的 p 值为 0.96,远大于常规的显著性水平 0.05。注意:这里的 p 值不需要显著 ,一个不显著的、大的 p 值才是我们期望看到的、证明模型稳健的“好结果”。
这意味着我们完全没有理由拒绝零假设。从统计学的角度来看,我们得出的结论是:这个安慰剂处理的效应确实为 0 。
这是一个非常理想和正面的结果,增强了原始结论的可信度。
这个检验达到了预期效果。当将一个本身不应产生任何因果效应的“安慰剂”变量喂给模型时,模型正确地识别出它的效应为零。
这说明您的因果模型并非一个“胡乱寻找关联”的黑箱。它具备了相当的辨别能力:
对于真实的处理变量 (different_room_assigned),它估算出-了-个显著且不为零的效应 (-0.2621)。
对于虚假的安慰剂变量 ,它正确地估算出了一个为零的效应。
因此,可以得出结论:原始因果估算是稳健的 。它成功通过了“安慰剂处理”这一严格的检验,这让我们更有信心相信,最初发现的 -0.2621 这个效应值,反映的是一个真实的因果关系,而不仅仅是数据中的某种随机巧合或虚假关联。
方法三,数据子集反驳器 数据子集反驳器:创建数据的子集(类似于交叉验证),并检查因果估算在不同子集之间是否有所变化。如果假设是正确的,因果估算应该不会有太大变化。
1 2 3 4 5 6 7 8 9 refute3_results = model.refute_estimate( identified_estimand, estimate, method_name = "data_subset_refuter" ) print (refute3_results)
1 2 3 4 Refute: Use a subset of data Estimated effect:-0.2621202162797218 New effect:-0.2620885527105116 p value:0.96
这个反驳结果使用了 数据子集反驳器 (Data Subset Refuter) 的方法。它的核心思想是检验您的因果估算结果是否对数据的微小变动敏感。如果一个因果关系是真实且普遍存在的,那么它不应该因为随机移除了数据中的一小部分样本而发生剧烈改变。
检验过程是:dowhy 默认会随机抽取您原始数据的 90% 形成一个子集,然后在这个子集上完整地重新运行一次因果效应估算,并比较新旧结果的差异。
Estimated effect (-0.2621202162797218): 这是在完整数据集上得到的原始因果效应估算值。表示分配不同房间会导致取消率平均下降 26.21%。
New effect (-0.2620885527105116): 这是在随机抽取的 90% 数据子集上重新计算出的因果效应值。可以看到,这个新效应值与原始效应值非常接近。
原始值:-0.26212
新数值:-0.26208
两者差异极小,仅为 0.00003 左右。这直观地表明,即使丢失了 10% 的随机数据,结论也几乎保持不变。
p value (0.96): 这个 p 值检验的“零假设”是:“原始效应值与新效应值之间的差异为零” 。
p 值为 0.96,这是一个非常大的值,远高于 0.05 的显著性水平。
这意味着,我们完全没有统计学上的理由认为这两个效应值有任何显著差异。它们之间的微小差别,完全可以解释为因随机抽样而产生的正常波动。
这个检验就像是在对您的结论进行“压力测试”。如果结论仅仅依赖于数据中少数几个特殊的、具有高影响力的点 (outliers),那么当这些点被随机移除时,结果就会发生剧变。
结果成功通过了这个测试,结论在数据子集上保持了高度的一致性,这说明:因果效应估算不是一个脆弱的、一点就破的“巧合”,而是稳定的;因果关系似乎普遍存在于数据样本中,而不是由一小撮异常数据驱动的。
综合结论 综合来看,已经成功通过了三个非常关键的反驳检验:
随机共同原因 :证明模型对无关噪声不敏感。安慰剂处理 :证明模型能正确识别“无效应”的情况。数据子集 :证明结果不依赖于少数特定数据点,具有稳定性。
每通过一个检验,对原始因果效应 -0.2621 的信心就增加一分。到目前为止,所有的证据都强烈支持您的结论:分配不同房间确实是导致预订取消率下降的一个重要原因,其效应大小约为 26.21 个百分点,并且这个结论是稳健、可靠的。
完整代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 import pandas as pddataset = pd.read_csv('Z:/TData/big-data/SADAGY/251021_causal_inference_booking_cancellation.csv' ) if False : dataset.head() dataset.columns dataset['total_stay' ] = dataset['stays_in_week_nights' ] + dataset['stays_in_weekend_nights' ] dataset['guests' ] = dataset['adults' ] + dataset['children' ] + dataset['babies' ] dataset['different_room_assigned' ] = 0 slice_indices = dataset['reserved_room_type' ] != dataset['assigned_room_type' ] dataset.loc[slice_indices, 'different_room_assigned' ] = 1 dataset = dataset.drop(['stays_in_week_nights' , 'stays_in_weekend_nights' , 'adults' , 'children' , 'babies' , 'reserved_room_type' , 'assigned_room_type' ], axis = 1 ) if False : dataset.columns dataset.isnull().sum () dataset = dataset.drop(['agent' , 'company' ], axis = 1 ) dataset['country' ] = dataset['country' ].fillna(dataset['country' ].mode()[0 ]) dataset = dataset.drop(['reservation_status' , 'reservation_status_date' , 'arrival_date_day_of_month' ], axis = 1 ) dataset = dataset.drop(['arrival_date_year' ], axis = 1 ) dataset = dataset.drop(['distribution_channel' ], axis = 1 ) dataset['different_room_assigned' ] = dataset['different_room_assigned' ].replace(1 , True ) dataset['different_room_assigned' ] = dataset['different_room_assigned' ].replace(0 , False ) dataset['is_canceled' ] = dataset['is_canceled' ].replace(1 , True ) dataset['is_canceled' ] = dataset['is_canceled' ].replace(0 , False ) dataset.dropna(inplace = True ) if False : dataset.columns dataset.iloc[:, 5 :20 ].head(100 ) dataset = dataset[dataset.deposit_type == "No Deposit" ] dataset.groupby(['deposit_type' , 'is_canceled' ]).count() dataset_copy = dataset.copy(deep = True ) if False : counts_sum = 0 for i in range (1 , 10000 ): counts_i = 0 rdf = dataset.sample(1000 ) counts_i = rdf[rdf["is_canceled" ] == rdf["different_room_assigned" ]].shape[0 ] counts_sum += counts_i counts_sum / 10000 if False : counts_sum = 0 for i in range (1 , 10000 ): counts_i = 0 rdf = dataset[dataset["booking_changes" ] == 0 ].sample(1000 ) counts_i = rdf[rdf["is_canceled" ] == rdf["different_room_assigned" ]].shape[0 ] counts_sum += counts_i counts_sum / 10000 if False : counts_sum = 0 for i in range (1 , 10000 ): counts_i = 0 rdf = dataset[dataset["booking_changes" ] > 0 ].sample(1000 ) counts_i = rdf[rdf["is_canceled" ] == rdf["different_room_assigned" ]].shape[0 ] counts_sum += counts_i counts_sum / 10000 if True : import dowhy from IPython.display import Image, display causal_graph = '''digraph { different_room_assigned[label="Different Room Assigned"]; is_canceled[label="Booking Cancelled"]; booking_changes[label="Booking Changes"]; previous_bookings_not_canceled[label="Previous Booking Retentions"]; days_in_waiting_list[label="Days in Waitlist"]; lead_time[label="Lead Time"]; market_segment[label="Market Segment"]; country[label="Country"]; U[label="Unobserved Confounders",observed="no"]; is_repeated_guest; total_stay; guests; meal; hotel; U->{different_room_assigned,required_car_parking_spaces,guests,total_stay,total_of_special_requests}; market_segment -> lead_time; lead_time->is_canceled; country -> lead_time; different_room_assigned -> is_canceled; country->meal; lead_time -> days_in_waiting_list; days_in_waiting_list ->{is_canceled,different_room_assigned}; previous_bookings_not_canceled -> is_canceled; previous_bookings_not_canceled -> is_repeated_guest; is_repeated_guest -> {different_room_assigned,is_canceled}; total_stay -> is_canceled; guests -> is_canceled; booking_changes -> different_room_assigned; booking_changes -> is_canceled; hotel -> {different_room_assigned,is_canceled}; required_car_parking_spaces -> is_canceled; total_of_special_requests -> {booking_changes,is_canceled}; country->{hotel, required_car_parking_spaces,total_of_special_requests}; market_segment->{hotel, required_car_parking_spaces,total_of_special_requests}; }''' model = dowhy.CausalModel( data = dataset, graph = causal_graph.replace("\n" , " " ), treatment = "different_room_assigned" , outcome = 'is_canceled' ) model.view_model(file_name = 'C:/Users/Administrator/Desktop/causal_model' ) display(Image(filename = "C:/Users/Administrator/Desktop/causal_model.png" )) if True : identified_estimand = model.identify_effect(proceed_when_unidentifiable = True ) print (identified_estimand) if True : estimate = model.estimate_effect( identified_estimand, method_name = "backdoor.propensity_score_weighting" , target_units = "ate" ) print (estimate) if True : if True : refute1_results = model.refute_estimate( identified_estimand, estimate, method_name = "random_common_cause" ) print (refute1_results) if True : refute2_results = model.refute_estimate( identified_estimand, estimate, method_name = "placebo_treatment_refuter" ) print (refute2_results) if True : refute3_results = model.refute_estimate( identified_estimand, estimate, method_name = "data_subset_refuter" ) print (refute3_results)